what transformaion have occured to create function f(x)=3x^3-4
Parent Functions And Transformations
Parent Functions: When you hear the term parent function, you may be inclined to think of two functions who love each other very much creating a new function. The similarities don't end there! In the same style that nosotros share like characteristics, genes, and behaviors with our ain family, families of functions share similar algebraic properties, take like graphs, and tend to acquit alike.
Read Also: How To Employ Sohcahtoa?
An instance of a family of functions is the quadratic functions. All quadratic functions accept the highest exponent of ii, their graphs are all parabolas so they have the same shape, and they all share sure characteristics. Well, that's non exactly right; however, at that place are some similarities that we can observe between our own parents and parent functions. In mathematics, we have certain groups of functions that are called families of functions. Just like our own families have parents, families of functions also accept a parent function.

Parent Functions Worksheet
*TheGreatest IntegerFunction, sometimes called theStep Function, returns the greatest integer less than or equal to a number (call back of rounding downwardly to an integer). There's also aTo the lowest degree IntegerFunction, indicated by \(y=\left\lceil x \right\rceil \), which returns the least integer greater than or equal to a number (call back of rounding up to an integer).
Once more, the "parent functions" presume that we have the simplest class of the function; in other words, the function either goes through the origin \(\left( {0,0} \right)\) or if it doesn't go through the origin, it isn't shifted in any manner.
Notes on Cease Beliefs: To go theend beliefs of a function, we just look at thesmallest andlargest values of \(x\), and see which manner the \(y\) is going. Non all functions take end behavior defined; for example, those that go back and forth with the \(y\) values and never really go style up or fashion down (called "periodic functions") don't have finish behaviors.
Virtually of the fourth dimension, our end behavior looks something like this:\(\displaystyle \begin{array}{l}ten\to -\infty \text{, }\,y\to \,\,?\\x\to \infty \text{, }\,\,\,y\to \,\,?\end{array}\) and we have to fill up in the \(y\) role. So the terminate behavior for a line with a positive slope is: \(\begin{array}{l}ten\to -\infty \text{, }\,y\to -\infty \\x\to \infty \text{, }\,\,\,y\to \infty \end{assortment}\).
There are a couple of exceptions; for instance, sometimes the \(x\) starts at0 (such as in theradical function), we don't have the negative portion of the \(10\) end behavior. Also, when \(10\) starts very close to0 (such as in in thelog function), nosotros point that \(x\) is starting from the positive (right) side of0 (and the \(y\) is going downwardly); nosotros indicate this by \(\displaystyle x\to {{0}^{+}}\text{, }\,y\to -\infty \).
eight Parent Functions
- The Exponential Office is f(x)=e.
- x.
- The Linear Function is f(x)=10.
- viii Parent Functions.
- The Logistic Function is f(x)= 1. ane+e.
- Looking for boundedness.
- The Cubing Office is f(x)=10.
- The Cosine Function is f(x)=cos x.
What is an instance of a parent office?
Anexample of a family unit offunctions is the quadratic functions. … Aparent part is the simplestfunction that even so satisfies the definition of a certain type ofrole. Forexample, when we think of the linearfunctions which make upwards a family offunctions, theparent function would be y = ten.
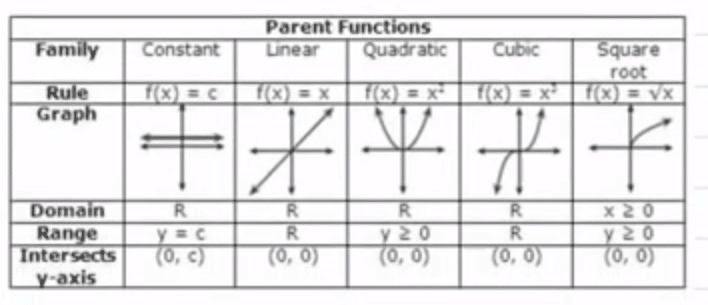
Parent Functions Graphs
Includes basic parent functions for linear, quadratic, cubic, rational, absolute value, and square root functions.
Lucifer graphs to equations. Match family names to functions. Match graphs to the family names. Read cards carefully so that yous match them correctly.
This is designed to be a matching activity. Information technology will non work well as a flashcard activeness.
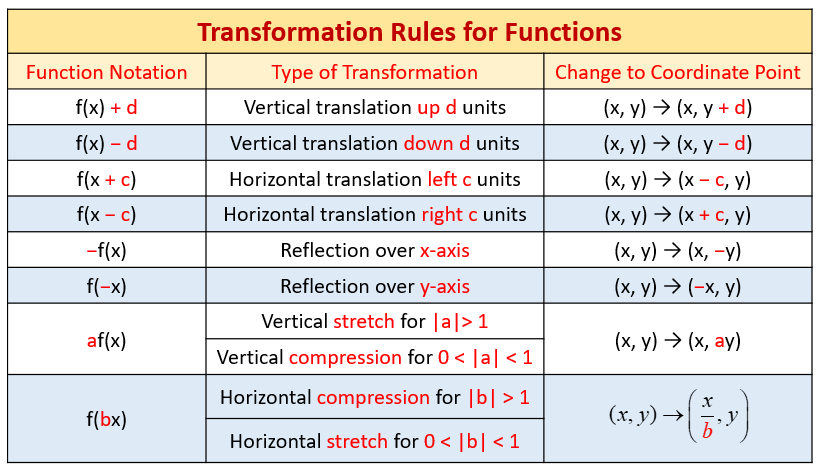
The following table shows the transformation rules for functions. Scroll down the page for examples and solutions on how to use the transformation rules.
Parent Functions Chart
T-charts are extremely useful tools when dealing with transformations of functions. For case, if y'all know that the quadratic parent office \(y={{ten}^{2}}\) is being transformedii units to the right, and1 unit down (simply a shift, not a stretch or a flip yet), we tin can create the original t-chart, following by the transformation points on the outside of the original points. Then nosotros can plot the "exterior" (new) points to go the newly transformed function:
| Transformation | T-chart | Graph | ||||||||
| Quadratic Function \(y={{x}^{2}}\) Transform part2 units to the right, and1 unit of measurement down. |
Transformed: Domain: \(\left( {-\infty ,\infty } \right)\) Range: \(\left[ {-1,\,\,\infty } \right)\) |  |
When looking atthe equation of the moving function, withal, we have to exist careful.
When functions are transformed on theexterior of the \(f(ten)\) part, you move the function upwardly and down and practise the "regular" math, as we'll run across in the examples below. These areverticaltransformations ortranslations, and bear upon the \(y\) office of the part.
When transformations are made on the within of the \(f(ten)\) part, you move the functionback and forth (only practise the "opposite" math – since if you were to isolate the ten , yous'd movement everything to the other side). These arehorizontal transformationsor translations, and affect the \(x\) part of the function.
There are several ways to perform transformations of parent functions; I like to uset -charts since they piece of work consistently with ever function. And note that in virtually t-charts, I've included more than than just thedisquisitional points above, only to prove the graphs better.
Parent Functions And Transformations Worksheet
Equally mentioned above, each family unit of functions has a parent function. Aparent function is the simplest role that still satisfies the definition of a certain type of office. For example, when nosotros think of the linear functions which make up a family of functions, the parent function would bey =x. This is the simplest linear office.
Furthermore, all of the functions inside a family unit of functions tin be derived from the parent office by taking the parent part's graph through various transformations. These transformations include horizontal shifts, stretching, or compressing vertically or horizontally, reflecting over the ten ory axes, and vertical shifts. For example, in the above graph, we encounter that the graph ofy = 2x^2 + 4ten is the graph of the parent functiony =ten^two shifted one unit to the left, stretched vertically, and shifted down two units. These transformations don't change the full general shape of the graph, so all of the functions in a family unit take the same shape and expect similar to the parent role.
Algebraically, these transformations represent to adding or subtracting terms to the parent part and to multiplying past a constant. For instance, the functiony = 2x^2 + 4x can be derived by taking the parent officey =x^2, multiplying it by the constant 2, then adding the term 4x to it.
Read Also: What Are Agents of Socialization?
Source: https://educationisaround.com/parent-functions/
0 Response to "what transformaion have occured to create function f(x)=3x^3-4"
Post a Comment